iopstorm.blogg.se - Mass moment of inertia of a circle with radius of gyration

Mass moment of inertia of a circle with radius of gyration free#

Area Moment of Inertia - Typical Cross Sections I - Typical cross sections and their Area Moment of Inertia.American Wide Flange Beams - American Wide Flange Beams ASTM A6 in metric units.Statics - Loads - force and torque, beams and columns.Mechanics - Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.Dynamics - Motion - velocity and acceleration, forces and torques.Basics - The SI-system, unit converters, physical constants, drawing scales and more.Moments of Inertia for a slender rod with axis through end can be expressed as Moments of Inertia for a slender rod with axis through center can be expressed as Moments of Inertia for a rectangular plane with axis along edge can be expressed as Moments of Inertia for a rectangular plane with axis through center can be expressed as R = radius in sphere (m, ft) Rectangular Plane R = distance between axis and hollow (m, ft) Solid sphere R = distance between axis and outside disk (m, ft) Sphere Thin-walled hollow sphere R = distance between axis and outside cylinder (m, ft) Circular Disk R o = distance between axis and outside hollow (m, ft) Solid cylinder R i = distance between axis and inside hollow (m, ft) R o = distance between axis and outside hollow (m, ft) Hollow cylinder R = distance between axis and the thin walled hollow (m, ft) Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass (1) and can be expressed as: Some Typical Bodies and their Moments of Inertia Cylinder Thin-walled hollow cylinder Radius of Gyration in Structural Engineering

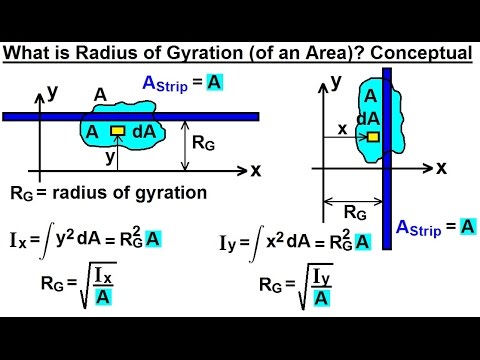
I = moment of inertia for the body ( kg m 2, slug ft 2) The Radius of Gyration for a body can be expressed as The Radius of Gyration is the distance from the rotation axis where a concentrated point mass equals the Moment of Inertia of the actual body. K = inertial constant - depending on the shape of the body Radius of Gyration (in Mechanics) + m n r n 2 (2)įor rigid bodies with continuous distribution of adjacent particles the formula is better expressed as an integralĭm = mass of an infinitesimally small part of the body Convert between Units for the Moment of InertiaĪ generic expression of the inertia equation is I = ∑ i m i r i 2 = m 1 r 1 2 + m 2 r 2 2 +. Point mass is the basis for all other moments of inertia since any object can be "built up" from a collection of point masses. = 1 kg m 2 Moment of Inertia - Distributed Masses The Moment of Inertia with respect to rotation around the z-axis of a single mass of 1 kg distributed as a thin ring as indicated in the figure above, can be calculated as

Mass moment of inertia of a circle with radius of gyration free#

Make 3D models with the free Engineering ToolBox Sketchup Extension R = distance between axis and rotation mass (m, ft) Example - Moment of Inertia of a Single Mass I = moment of inertia ( kg m 2, slug ft 2, lb f fts 2)

Moment of Inertia of a body depends on the distribution of mass in the body with respect to the axis of rotationįor a point mass the Moment of Inertia is the mass times the square of perpendicular distance to the rotation reference axis and can be expressed as.

Moment of Inertia has the same relationship to angular acceleration as mass has to linear acceleration. Let us consider a rigid body consisting of n particles of masses m₁, m₂, m₃, …, mₙ which lie at distance r₁, r₂, r₃, …, rₙ respectively from the axis of rotation XY as shown in figure.Mass Moment of Inertia (Moment of Inertia) - I - is a measure of an object's resistance to change in rotation direction. Mathematically, it is the product of mass and square of distance from the axis of rotation. It tries to maintain the original state of the body unless an external torque is applied. Moment of inertia of a body is its property which keeps it in its own position of rest or in uniform circular motion in rotational dynamics.

Moment of Inertia in rotational motion is same as the mass in linear motion. Relation of Moment of Inertia with Torque.